――あなたの情報力を試すサイト。
最新記事
(04/17)
(04/13)
(04/08)
(03/25)
(03/24)
プロフィール
HN:
yoh
性別:
非公開
職業:
ソフトウェア開発業
趣味:
テニス、美術鑑賞、ひとり旅、オタク系全般
自己紹介:
しがない自営業のプログラマです。
ブログ内検索
アクセス解析
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
例題
とてもシンプルな例題です。真偽について考察してください。
「古代ローマ人は、人殺しをした」
→「セネカは古代ローマ人である(ここまでは事実とする)」
→「なので、古代ローマ人であるセネカもまた人殺しである」
――果たして、是か非か?
じつは――
上記の例題は意地悪問題です。なぜなら1つ目の文章が2つの意味に取れるからです。
a・「少なくとも1人以上の古代ローマ人は、人殺しをした」
b・「全ての古代ローマ人は、人殺しをした」
もしbが真であればセネカも人殺しですが、aのみが真であればそうではありません。
解説
「少なくとも1人以上の○○が~であること」と、「全ての○○が~であること」は厳密に区別しなくてはいけません。
数学(論理学)の世界では両者を「∃」と「∀」という記号で区別します。わざわざ記号があるくらいですから、それだけこの区別が重要だということは察しがつきます。
a・「∃古代ローマ人は、人殺しをした」
b・「∀古代ローマ人は、人殺しをした」
これまた数学用語で「集合」という言葉がありますが、「ローマ人」という「集合」の中に「セネカ」が「要素」として含まれていることになります。
もしbが真であれば、
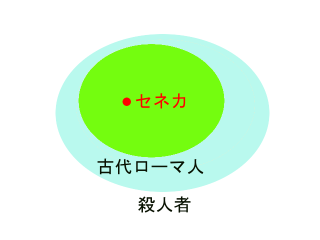
「殺人者」という大きな集合の中に「ローマ人」という集合全体が含まれるわけですから、「セネカ」も「殺人者」に含まれます。
一方、もしaのみが真であれば、
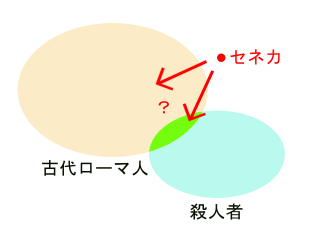
「ローマ人」と「殺人者」という別々の集合があり、なおかつ両方に属する「積集合」があるということだけが言えます。「ローマ人でなおかつ殺人者」という「積集合」の中に「セネカ」が含まれているかどうかは分かりません。
しかし、うっかりしていると「∃と∀を混同」してしまって、bでなくaのみが真であるのに「セネカも殺人者である」かのように錯覚してしまったり、酷い場合には「古代ローマ人全員が殺人者である」と極論してしまったりすることになります。
ちょっと待った!
例えばこういう例。
・○月×日の△△行きツアーに参加した10人のうち、1人は田中さんだった。
・参加者10人のうち9人が食中毒になったが、1人は食中毒にならなかった。
について、
1・「全ての参加者が食中毒になったわけではない」
→「なので、現時点では田中さんが食中毒になったとは限らない」
と言うことは可能です(これが今回のテーマ)。しかし、
2・「全ての参加者が食中毒になったわけではない」
→「なのでこのツアーと食中毒は関係ない」
とは言えません(今回のテーマの対象外)。∃と∀を厳密に区別して考えることは、入手した情報の持つ意味そのものを正しく理解するために必要です。しかし、その事実から何が類推出来るかとなると、別問題です。
筆者の見解
それでも「∃と∀の混同」は避けるべきです。そもそも与えられた情報の意味を間違って解釈してしまってはどうしようもないからです。
途中の理屈がどれだけ正しくても、推論の土台となる情報についてその意味を間違って解釈しているのでは正しい結論が得られるはずもありません。
また、「∃と∀の混同」は意図的に煽動に用いることが出来るため、その点でも警戒した方がよいです。詳細はこちら。
演習
「少なくとも1人の○○は~である」
「全ての○○は~である」
○○と~に自由に単語を当て嵌め、少なくとも3つ文章を作ってください。
※その後、こちらを。
とてもシンプルな例題です。真偽について考察してください。
「古代ローマ人は、人殺しをした」
→「セネカは古代ローマ人である(ここまでは事実とする)」
→「なので、古代ローマ人であるセネカもまた人殺しである」
――果たして、是か非か?
じつは――
上記の例題は意地悪問題です。なぜなら1つ目の文章が2つの意味に取れるからです。
a・「少なくとも1人以上の古代ローマ人は、人殺しをした」
b・「全ての古代ローマ人は、人殺しをした」
もしbが真であればセネカも人殺しですが、aのみが真であればそうではありません。
解説
「少なくとも1人以上の○○が~であること」と、「全ての○○が~であること」は厳密に区別しなくてはいけません。
数学(論理学)の世界では両者を「∃」と「∀」という記号で区別します。わざわざ記号があるくらいですから、それだけこの区別が重要だということは察しがつきます。
a・「∃古代ローマ人は、人殺しをした」
b・「∀古代ローマ人は、人殺しをした」
これまた数学用語で「集合」という言葉がありますが、「ローマ人」という「集合」の中に「セネカ」が「要素」として含まれていることになります。
もしbが真であれば、
「殺人者」という大きな集合の中に「ローマ人」という集合全体が含まれるわけですから、「セネカ」も「殺人者」に含まれます。
一方、もしaのみが真であれば、
「ローマ人」と「殺人者」という別々の集合があり、なおかつ両方に属する「積集合」があるということだけが言えます。「ローマ人でなおかつ殺人者」という「積集合」の中に「セネカ」が含まれているかどうかは分かりません。
しかし、うっかりしていると「∃と∀を混同」してしまって、bでなくaのみが真であるのに「セネカも殺人者である」かのように錯覚してしまったり、酷い場合には「古代ローマ人全員が殺人者である」と極論してしまったりすることになります。
ちょっと待った!
例えばこういう例。
・○月×日の△△行きツアーに参加した10人のうち、1人は田中さんだった。
・参加者10人のうち9人が食中毒になったが、1人は食中毒にならなかった。
について、
1・「全ての参加者が食中毒になったわけではない」
→「なので、現時点では田中さんが食中毒になったとは限らない」
と言うことは可能です(これが今回のテーマ)。しかし、
2・「全ての参加者が食中毒になったわけではない」
→「なのでこのツアーと食中毒は関係ない」
とは言えません(今回のテーマの対象外)。∃と∀を厳密に区別して考えることは、入手した情報の持つ意味そのものを正しく理解するために必要です。しかし、その事実から何が類推出来るかとなると、別問題です。
筆者の見解
それでも「∃と∀の混同」は避けるべきです。そもそも与えられた情報の意味を間違って解釈してしまってはどうしようもないからです。
途中の理屈がどれだけ正しくても、推論の土台となる情報についてその意味を間違って解釈しているのでは正しい結論が得られるはずもありません。
また、「∃と∀の混同」は意図的に煽動に用いることが出来るため、その点でも警戒した方がよいです。詳細はこちら。
演習
「少なくとも1人の○○は~である」
「全ての○○は~である」
○○と~に自由に単語を当て嵌め、少なくとも3つ文章を作ってください。
※その後、こちらを。
では次に、ではその3つの文章の○○と~を
「少なくとも1人の○○は~であるからと言って、全ての○○は~であるとは言えない」
という文に当て嵌めてみてください。
PR
この記事にコメントする
※実在の個人、集団についてのコメントはご遠慮ください。
